Tree

基本概念

• 根节点；
• 父节点&子节点（0 ~ n）(无子节点被称为叶子节点)&堂兄弟节点；
• 节点的度：其子节点的数目；
• 树的度：max(节点的度)；
• 树的高度：树的最大深度；
• 结点的层次：从 1 开始，到该节点的层数为 n，其高度为(最远的叶子节点的层数-n)，则其子节点深度为 n+1 层。

二叉树

每个节点最多两个子节点，分别为左右子节点。

单节点树

只有根节点。

空二叉树

没有任何节点（包括根节点）

左(右)斜树

所有节点只有左(右)节点。

满二叉树

最下方叶子节点没有左右节点，除此之外的节点都有左右子节点。

完全二叉树

最下一层的叶子节点可以为空，其余节点必须填满，并且叶子节点靠左排列。（满二叉树从叶子层开始，由右侧开始，不断删除，一直也满足完全二叉树）。

数组储存

从左到右依次编号，从 0 开始

int tree[8] = {0, 1, 2, 3, 4, 5, 6, 7, 8};

When i>0： 节点 i 的双亲下标为floor((i-1)/2);；
When 2*i+1<n： 节点 i 的左子节点下标为 2*i+1，否则无左子节点。
When 2*i+2<n： 节点 i 的右子节点下标为 2*i+2，否则无右子节点。

因此，我们可以看出来：所有左节点都为奇数索引，而右节点都为偶数索引。

用数组存储二叉树的时候，要求节点位置和数组索引之间有明确映射关系，是按照完全 or 满二叉树的形态设计的。若不是则可能浪费空间，因为不存在的节点需要在数组留空。

链式存储

二叉树中，每个节点都有数据域和左右两个指针域。两个指针分别指向左右子节点，无则设为NULL。

若二叉树节点数量：n

分支数：n-1 指针域数量：2*n
非空指针域：n-1
空指针域：n+1 若为完全二叉树，则深度：floor(log n)+1

非空二叉树第 i 层最多节点数：2^(i-1)
深度为 h 的非空二叉树最多节点：2^h-1
非空二叉树有 a 个叶节点，有 b 个度为 2 的节点，则 a=b+1
推论：n[0]=n[2]+2n[3]+···+(m-1)n[m]+1

树的创建

分为逐层创建和深度优先创建。

逐层：1223333…… 深度：1233233……

前者推荐用队列，后者推荐用递归。

// 逐层建立(BFS)
 
// 深度优先建立
node *treeCreate(void)
{
    char ch = getchar();
    if (ch == '^' || ch == EOF)
        return NULL;
    node *root = (node *)malloc(sizeof(node));
    root->data = ch;
    root->left = treeCreate();
    root->right = treeCreate();
    return root;
}
 

树的遍历

前序遍历
顺序：根→左→右

中序遍历 顺序：左→根→右

后序遍历 顺序：左→右→根

递归遍历

/*root->left表明去找左节点，右节点同理，printf表明访问当前节点，也就是“根”。*/
typedef struct node
{
    int data;
    struct node *left;
    struct node *right;
} node;
 
// DFS
 
// 递归：
// 前序遍历：
void preOrder(node *root)
{
    if (root == NULL)
        return;
    printf("%d ", root->data);
    preOrder(root->left);
    preOrder(root->right);
}
// 中序遍历：
void inOrder(node *root)
{
    if (root == NULL)
        return;
    inOrder(root->left);
    printf("%d ", root->data);
    inOrder(root->right);
}
// 后序遍历：
void postOrder(node *root)
{
    if (root == NULL)
        return;
    postOrder(root->left);
    postOrder(root->right);
    printf("%d ", root->data);
}
 
// 非递归：
// 前序遍历：
void preOrder(node *root)
{
    if (root == NULL)
        return;
    node *stack[105] = {root};
    int top = 0;
    while (top >= 0)
    {
        node *p = stack[top--];
        printf("%d ", p->data);
        if (p->right != NULL)
            stack[++top] = p->right;
        if (p->left != NULL)
            stack[++top] = p->left;
    }
}
// 中序遍历
void inOrder(node *root)
{
    if (root == NULL)
        return;
    node *stack[105];
    int top = -1;
    node *p = root;
    while (p != NULL || top != -1)
    {
        while (p != NULL)
        {
            stack[++top] = p;
            p = p->left;
        }
        p = stack[top--];
        printf("%d ", p->data);
        p = p->right;
    }
}
// 后序遍历
void postOrder(node *root)
{
    if (root == NULL)
        return;
    node *stack[105];
    int top = -1;
    node *p = root, *l = NULL;
    while (p != NULL || top != -1)
    {
        while (p != NULL)
        {
            stack[++top] = p;
            p = p->left;
        }
        if (stack[top]->right != NULL && l != stack[top]->right)
            p = stack[top]->right;
        else
        {
            p = stack[top--];
            printf("%d ", p->data);
            l = p;
        }
    }
}
 
 
// 层次遍历(BFS)
void layOrder(node *root)
{
    if (root == NULL)
        return;
    node *queue[100] = {root};
    int front = 0, rear = 0;
    while (front <= rear)
    {
        node *p = queue[front++];
        printf("%d ", p->data);
        if(p->left!=NULL)
            queue[rear++] = p->left;
        if(p->right!=NULL)
            queue[rear++] = p->right;
    }
}

事实上，递归的开发效率更高。而非递归更安全且高效。递归程序都可以如上，
使用显式的“栈”这一结构，储存状态、执行顺序，从而模拟递归，转化为非递归程序。

其他操作

树的复制、删除、高深度：用递归即可。

其他种类的二叉树

哈夫曼编码(哈夫曼树)

线索二叉树

如何添加线索？

Node *prior = NULL;
Node *Head = (Node *)malloc(sizeof(Node));
Head->lmark = 0, Head->lc = root;
prior = Head;
 
void inThread(Node *root)
{
    if (!root)
        return;
    inThread(root->lc); // 线索化左子节点
    if (!root->lc)
        root->lmark = 0, root->lc = prior; // 若是叶子，指向前驱prior
    else
        root->lmark = 1;
    if (!prior->rc)
        prior->rmark = 0, prior->rc = root; // 若是叶子，指向后继root
    else
        prior->rmark = 1;
    prior = root; // 更新前驱为当前位置
    inThread(root->rc); // 线索化右子节点
}
 
prior->rmark = 0, prior->rc = Head;
Head->rmark = 0, Head->rc = prior;

prior 与 root 是前驱和后继的关系，所以就仿佛我们遍历链表一样，prior 紧跟着 root，root 每次右移之前都更新为 root。
我们是按照先左边、再中间、后右边的顺序处理节点的，正如中序遍历。因为添加线索的过程就是一边遍历，一边改指针。
这也就是说，我们相当于在中序遍历树，只不过我们加了个 prior 记录前一个访问的节点，以便我们添加后继前驱关系。

Node *prior = NULL;
Node *Head = (Node *)malloc(sizeof(Node));
Head->lmark = 0, Head->lc = root;
prior = Head;
 
void inThread(node *root)
{
    if (root == NULL)
        return;
    node *stack[105];
    int top = -1;
    node *p = root;
    while (p != NULL || top != -1)
    {
        while (p != NULL)
        {
            stack[++top] = p;
            p = p->left;
        }
        p = stack[top--];
/*--------------------------------------------------------------------*/
        if (!root->lc)
	        root->lmark = 0, root->lc = prior; // 若是叶子，指向前驱prior
	    else
	        root->lmark = 1;
	    if (!prior->rc)
	        prior->rmark = 0, prior->rc = root; // 若是叶子，指向后继root
	    else
	        prior->rmark = 1;
	    prior = root; // 更新前驱为当前位置
/*--------------------------------------------------------------------*/
        p = p->right;
    }
}
 
prior->rmark = 0, prior->rc = Head;
Head->rmark = 0, Head->rc = prior;

我们仅仅是把 printf 改为建立关系，就得到了一个非递归版本，就是如此简单。 我们可以封装一下，毕竟定义一个 Head 节点，并且前后处理两次，十分繁杂，而且Do not repeat yourself.

Node* inTheader(Node *root)
{
	Node *Head = (Node *)malloc(sizeof(Node));
	Head->lmark = 0, Head->lc = root;
	Node *prior = Head;
	inThread(root);
	prior->rmark = 0, prior->rc = Head;
	Head->rmark = 0, Head->rc = prior;
	return Head;
}

注意：我们创建的线索树，头节点的左指针指着 root，右指针指着中序序列的最后一个节点。 这样，我们得到了一个“双向链表”：

• 正向：从 Head 一路向左开始遍历后继。
• 反向：从 Head 右指针所指节点开始遍历前驱。

  Maybe we can create a node with three pointer, so that we can store the address of the first node in a in-order? Quite Easy. Try it in yourself.

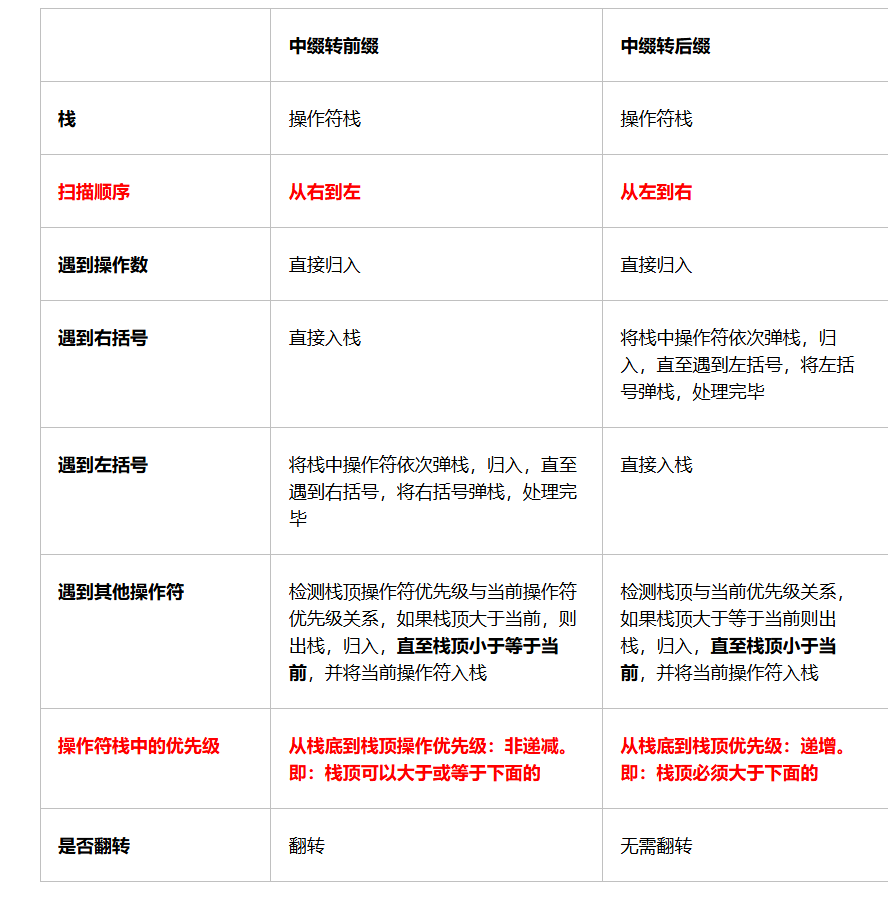
表达式树、前中后缀表达式