Tree is an important Data Abstraction for representing hierarchical relationships.
There we will consider a tree in a different perspective.
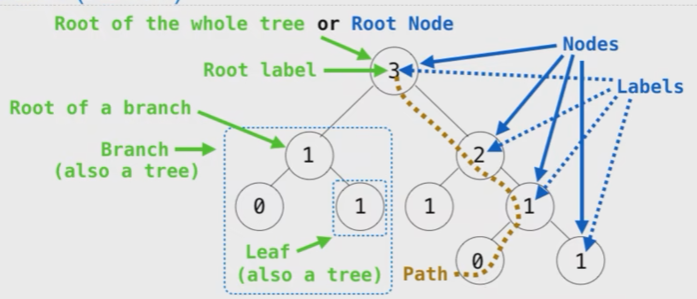
Definition
Recursive description (wooden trees):
A tree has a root label and a list of branches
Each branch is a tree
A tree with zero branches is called a leaf
Relative description (family trees):
Each location in a tree is called a node
Each node has a label that can be any value
One node can be the parent/child of another
People often refer to labels by their locations
Constructor
def tree(label, branches=[]):
for branch in branches:
assert is_tree(branch), 'branches must be a tree'
return [label] + list(branches)
def label(tree):
return tree[0]
def branches(tree):
return tree[1:]
def is_tree(tree):
if type(tree) != list or len(tree) < 1:
return False
for branch in branches(tree):
if not is_tree(branch):
return False
return True
def is_leaf(tree):
return not branches(tree)Tree processing
Functions that take trees as input or return trees as output are often tree recursive themselves.
- Processing a leaf is often the base case in a tree processing function.
- The recursive case typically makes a recursive call on each branch and then aggregates.
Example:
def count_leaves(t):
"""Count the leaves of a tree."""
if is_leaf(t):
return 1
else:
branch_counts = [count_leaves(b) for b in branches(t)]
return sum(branch_counts)
def leaves(t):
""""Return a list containing the leaf labels of tree."""
if is_leaf(t):
return [label(t)]
else:
branch_counts = [leaves(b) for b in branches(t)]
return sum(branch_counts,[])A function that creates a tree from another tree is typically also recursive
def increment_leaves(t):
"""Return a tree like t but with leaf labels incremented."""
if is_leaf(t):
return tree(label(t) + 1)
else:
bs = [increment_leaves(b) for b in branches(t)]
return tree(label(t), bs)
def increment(t):
"""Return a tree like t but with all labels incremented."""
return tree(label(t) + 1, [increment(b) for b in branches(t)])def print_tree(t, indent=0):
print(' ' * indent + str(label(t)))
for b in branches(t):
print_tree(b, indent+1)
There’s another type of Recursive Functions, sometimes handy.
def print_sums(t, so_far):
so_far = so_far + label(t)
if is_leaf(t):
print(so_far)
else:
for b in branches(t):
print_sums(b, so_far) Tree Class
class Tree:
"""A tree is a label and a list of branches."""
def __init__(self, label, branches=[]):
self.label = label
for branch in branches:
assert isinstance(branch, Tree)
self.branches = list(branches)
def __repr__(self):
if self.branches:
branch_str = ', ' + repr(self.branches)
else:
branch_str = ''
return 'Tree({0}{1})'.format(repr(self.label), branch_str)
def __str__(self):
return '\n'.join(self.indented())
def indented(self):
lines = []
for b in self.branches:
for line in b.indented():
lines.append(' ' + line)
return [str(self.label)] + lines
def is_leaf(self):
return not self.branches
def fib_tree(n):
"""A Fibonacci tree."""
if n == 0 or n == 1:
return Tree(n)
else:
left = fib_tree(n - 1)
right = fib_tree(n - 2)
fib_n = left.label + right.label
return Tree(fib_n, [left, right])
def leaves(t):
"""Return a list of leaf labels in Tree T."""
if t.is_leaf():
return [t.label]
else:
all_leaves = []
for b in t.branches:
all_leaves.extend(leaves(b))
return all_leaves
def height(t):
"""Return the number of transitions in the longest path in T."""
if t.is_leaf():
return 0
else:
return 1 + max([height(b) for b in t.branches])Tree Mutation
def prune(self, target):
self.branches = [b for b in self.branches if b.label != target]
for b in self.branches:
prune(b, target)