数制

数字抽象

数字系统用离散值变量表示信息。

N个状态的离散值表达的信息量位数（D：bit）为：
D = log N

bit for binary digit

数制

二进制

• base：2
• 十转二：反复除2，余数从右到左列出。

十六进制

• base：16
• 四位一组的二进制数可以表示一位十六进制数。
• 十转十六：反复除16，余数从右到左列出

转换

二进制对应：

• 八进制：三位一个数
• 十六进制：四位一个数

字节

• 8 bit is 1 Byte
• 字长指CPU一条指令一次可以处理的一块数据的宽度，64位处理器即8byte一字，32位处理器则4byte一字。
• 2^10=1024 K; 2^20约1,000,000 M; 2^30约1,000,000,000 G

LSB, MSB: 最低（高）有效字节/位数

加法

注意：

• 无符号数可根据最高位有无进位检测是否有溢出。
  • 可这样判断：对于 $te{m}_{\mathrm{32...0}}=a_{\mathrm{31...0}}+b_{\mathrm{31...0}}$, $tem[32]\ne 0$ 则溢出
• 有符号数判断依据为：相加两数符号相同且结果符号相反（即符号位变了）（0视为正数）
  • 可这样判断：对于 $te{m}_{\mathrm{32...0}}=a_{\mathrm{31...0}}+b_{\mathrm{31...0}}$, $tem[32]\ne tem[31]$ 则溢出

码

1. 原码：最高位是符号位，0 表示正数，1 表示负数。
2. 反码：正数的反码与原码相同；负数的反码是将原码除符号位外的所有位取反。（少见）
3. 补码：正数的补码与原码相同；负数的补码是其反码加 1。（计算机内部使用）
4. 移码：十进制值 + 偏移量，然后把结果作为二进制数写出。偏移量的主流选择是 $2^{n-1}$，浮点数的阶码用 $2^{n-1}-1$。移码的符号位与补码相反，数值位与补码完全相同。（用于快速比较，二进制直接比较即可得到真值大小关系）

对于补码，可以按位取反再加一，获得一个数的相反数。

• 符号扩展：把新加的位数全用符号位填满。
• 无符号扩展：把新加的位数全用 0 填满。

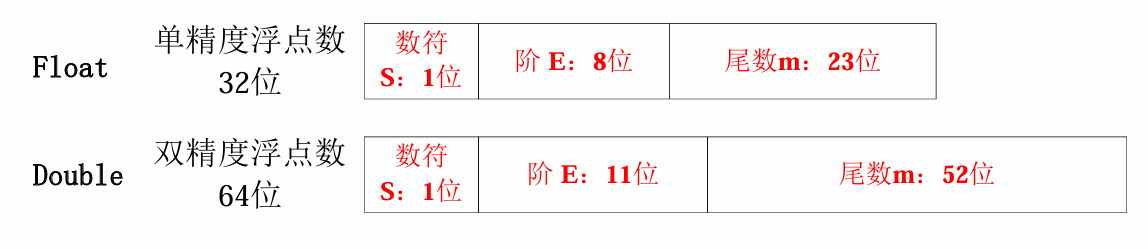
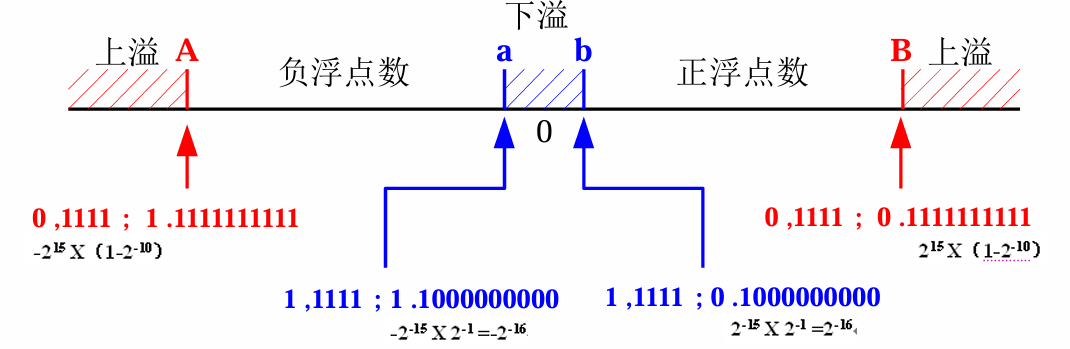
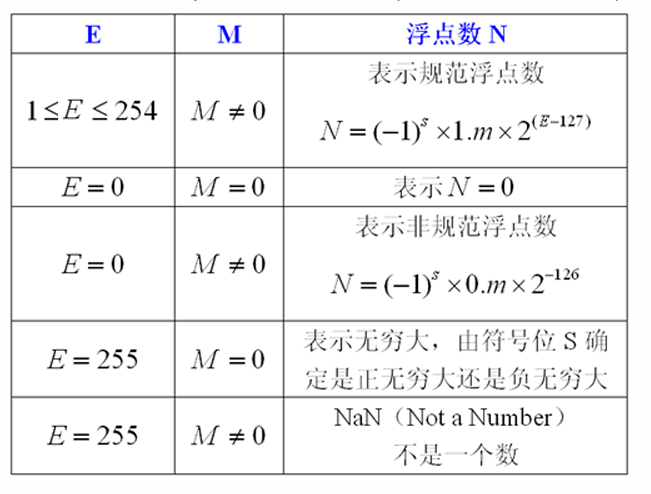
4. 浮点数（IEEE 754）
   • 阶码 E：采用定点整数表示，用移码表示，n 位阶码偏移量为 $2^{n-1}-1$。
   • 尾数 M：采用定点小数表示，尾数必须规格化成小数点左侧一定为1，并且小数点前面这个1作为隐含位被省略。这样单精度浮点数尾数实际上为24位。
   • 形式 $float=(-1{)}^S\times 1.m\times 2^{E-2^{n-1}}$